CosPro 5회차 9번 - 세 연산
22 Jul 2021문제
정수 number와 target이 주어졌을 때, 다음 세 연산을 이용해 number를 target으로 만들려 합니다.
연산 1. 1을 더합니다.
연산 2. 1을 뺍니다.
연산 3. 2를 곱합니다.
정수 number와 target이 매개변수로 주어질 때, number로 target으로 만들려면 연산을 최소 몇 번 해야 하는지 return 하도록 solution 메소드를 작성해 주세요.
매개변수 설명
두 정수 number와 target이 solution 메소드의 매개변수로 주어집니다.
- number와 target은 0 이상 10,000 이하입니다.
return 값 설명
number를 target으로 만들려면 연산을 최소 몇 번 해야 하는지 return 합니다.
풀이
접근1
전형적인 dp 라 생각하여 dp 배열안에 차례대로 첫 항을 넣고,
다음 값을 만드는 세 연산을 계산하여 점점 항을 늘려가는 식으로 접근하였다.
현재 항(dp[i])을 구하는 법을 다음과 같이 나누었다.
- 직전 항에서 더하기 연산 (
dp[i-1] + 1) - 절반 이전 항에서 곱하기 연산(
dp[i/2] + 1) - 다음 항에서 빼기 연산(
dp[i+1] + 1)
이 중 최소값을 찾으면 된다.
위 판별식을 만족하기 위해선 다음 항 이 미리 계산되어 있어야 한다.
이전 항(dp[i])들을 계산하고 그 인덱스의 두배에 해당하는 항(dp[i*2])에 값을 넣어준다.
쉽게 예시를 들면 6은 3에서 2를 곱한 값이다.
지금 계산하는 항이 3이라 하면 dp[3] 의 값을 구한 상태이다.
그렇다면 3에 [2를 곱하는 연산]을 적용하면 다음 항인 dp[6] = dp[3] + 1 이 될 것이다.
이렇게 다음 항을 미리 구해 놓을 수 있고, 다음 항에서 1을 뺀 값을 판별할 수 있는 것이다.
코드로 구현하면 다음과 같다.
int[] dp = new int[target+target+1];
for (int i = 0; i < dp.length; i++)
dp[i] = -1;
dp[number+1] = 1;
for (int i = number + 2; i <= target; i++) {
int min = i % 2 == 0 && i/2 >= number
? Math.min(dp[i-1]+1, dp[i/2]+1)
: dp[i-1]+1;
if (dp[i+1] != -1) {
min = Math.min(min, dp[i+1]+1);
}
if (dp[i] != -1) {
min = Math.min(min, dp[i]);
}
dp[i] = min;
dp[i*2] = min + 1;
}
dp 배열의 사이즈는 target 의 2배 길이 만큼 생성한다.
(2 연산에 의해 target2 의 인덱스가 계산이 되므로)
하지만 위의 코드에서는 문제가 생긴다.
1 부터 number 까지의 [-1 빼기 연산] 계산과, 해당 인덱스의 [*2 곱하기 연산] 계산이 누락되었기 때문이다.
예를 들면 다음과 같다. number = 5, target = 8 을 계산해보자.
(5 - 1) * 2 = 8 이와 같이 빼기 1번, 곱하기 1번으로 계산이 가능하다.
즉 시작점 5에서 뒤로가는 연산 (빼기연산)과 그 값의 곱하기 연산이 미리 계산되어 있어야 한다.
아래는 전체 코드이다.
public int solution(int number, int target) {
// 여기에 코드를 작성해주세요.
int answer = 0;
int[] dp = new int[target+target+1];
for (int i = 0; i < dp.length; i++)
dp[i] = -1;
for (int i = 1; i <= number; i++) {
dp[i] = number - i;
dp[i*2] = dp[i] + 1;
}
dp[number+1] = 1;
for (int i = number + 2; i <= target; i++) {
int min = i % 2 == 0 && i/2 >= number
? Math.min(dp[i-1]+1, dp[i/2]+1)
: dp[i-1]+1;
if (dp[i+1] != -1) {
min = Math.min(min, dp[i+1]+1);
}
if (dp[i] != -1) {
min = Math.min(min, dp[i]);
}
dp[i] = min;
dp[i*2] = min + 1;
}
return dp[target];
}
접근2
다른 방식의 접근이다.
대략적인 접근 방식은 다음과 같다.
- 연산이 사용되는 횟수를
depth라 칭한다. - 리스트를 생성하고
depth별로Set을 추가한다. Set안은depth(연산 횟수)에 따라 (미리)계산된 값들이 들어있다.Set을 활용하여 다음depth연산에 필요한 연산 값을 재사용 한다. (dp)
그림으로 표현하면 다음과 같다.
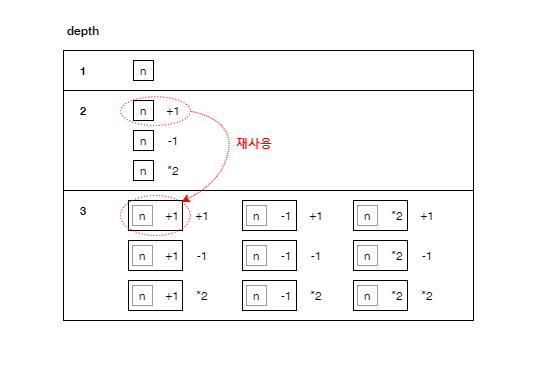
그림에서도 나타나듯이 직전 depth 에서 사용된 값이 다음 연산에서 재사용되는 것을 알 수 있다.
코드는 다음과 같다.
public int newSolution(int number, int target) {
if (number == target) return 0;
int depth = 1;
List<Set<Integer>> dp = new ArrayList<>();
Set<Integer> first = new HashSet<>();
first.add(number);
dp.add(0, new HashSet<>());
dp.add(1, first);
while (true) {
Set<Integer> newSet = new HashSet<>();
Set<Integer> preSet = dp.get(depth);
for (Integer preNode : preSet) {
for (int type = 1; type <= 3; ++type) {
int value = 0;
switch (type) {
case 1: value = preNode + 1; break;
case 2: value = preNode - 1; break;
case 3: value = preNode * 2; break;
}
if (value == target) return depth;
else newSet.add(value);
}
}
dp.add(newSet);
depth++;
}
}