Nzzi

프로그래머스 - N으로 표현

22 Jul 2021
Algorithm, dp


문제

아래와 같이 5와 사칙연산만으로 12를 표현할 수 있습니다.

12 = 5 + 5 + (5 / 5) + (5 / 5)
12 = 55 / 5 + 5 / 5
12 = (55 + 5) / 5

5를 사용한 횟수는 각각 6,5,4 입니다. 그리고 이중 가장 작은 경우는 4입니다.
이처럼 숫자 N과 number가 주어질 때, N과 사칙연산만 사용해서 표현 할 수 있는 방법 중 N 사용횟수의 최솟값을 return 하도록 solution 함수를 작성하세요.

제한사항

  • N은 1 이상 9 이하입니다.
  • number는 1 이상 32,000 이하입니다.
  • 수식에는 괄호와 사칙연산만 가능하며 나누기 연산에서 나머지는 무시합니다.
  • 최솟값이 8보다 크면 -1을 return 합니다.

풀이

dp 는 이전에 계산해놓은 것을 기억했다가 다음 계산에 사용하여 계산 효율을 극대화한다.
포인트는 다음 계산에는 이전 계산식이 반복되어야 한다는 점이다.

위 문제는 기본 사칙연산 외에도 숫자를 붙이는 괴랄한 연산이 포함된다.
5, 55, 555, 5555 … 쭉 증가하여 55555555 총 8개 까지

우선 사용되는 연산(사칙연산 + 괴랄한 연산)의 개수를 depth 로 표현하고 간단한 예시를 들어 그림을 그려보자.
depth 3 까지의 그림은 다음과 같다.

depth 별 연산 예시

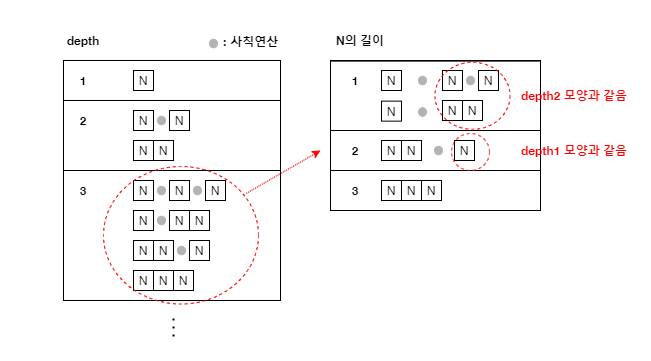
위 그림과 같이 반복되는 계산식을 확인할 수 있다.

depth = 3 의 예시에서 N의 길이가 1일 때는 depth = 2 의 계산식이 반복된다.
N의 길이가 늘어날 수록 그 이전 depth 가 사용되는 것을 확인할 수 있다.

위 반복을 다음과 같이 표현할 수 있게된다. (lengthOfN = N의 길이)
dp[lengthOfN] 사칙연산(+,-,*,/) dp[depth - lengthOfN]

dp 배열안에는 해당 depth 의 연산이 저장되어 있게 된다.

  • dp[1] (depth = 1이다, 즉 N을 1번써서 계산된 모든 결과값이 저장되어 있다)
    [N]
  • dp[2] (depth = 2이다, 즉 N을 2번써서 계산된 모든 결과값이 저장되어 있다)
    [NN], [N]+[N], [N]-[N], [N]*[N], [N]/[N]

즉 dp[lengthOfN] 사칙연산(+,-,*,/) dp[depth - lengthOfN] 이 의미하는 바는 다음과 같다.
앞부분 N의 길이에 해당하는 (미리 계산된) 결과값과 (dp[lengthOfN])
뒤부분 연산에 붙는 피연산자 (이 역시 미리 계산된) 결과값 (dp[depth - lengthOfN])
이 두 결과값을 카테시안 곱으로 사칙연산하여 계산하면 모든 조합을 나타낼 수 있게된다.

코드는 다음과 같다.

public int solution(int N, int number) {
    List<Set<Integer>> dp = new ArrayList<>();
    Set<Integer> first = new HashSet<>();
    if (N == number) return 1;
    first.add(N);
    dp.add(0, new HashSet<>());
    dp.add(1, first);

    for (int depth = 2; depth <= 8; depth++) {
        Set<Integer> newSet = new HashSet<>();
        for (int lengthOfN = 1; lengthOfN <= depth; lengthOfN++) {
            int value = 0;
            if (lengthOfN == depth) {
                value = convert(N, depth);
                if (value == number) return depth;
                else newSet.add(value);
            }
            else
                for (Integer preNode : dp.get(lengthOfN))
                    for (Integer postNode : dp.get(depth - lengthOfN))
                        for (int type = 1; type <= 4; type++) {
                            switch (type) {
                                case 1: value = preNode + postNode; break;
                                case 2: value = preNode - postNode; break;
                                case 3: value = preNode * postNode; break;
                                case 4: value = postNode != 0 ? preNode / postNode : -1; break;
                            }
                            if (type == 4 && postNode == 0) continue;
                            if (value == number) return depth;
                            else newSet.add(value);
                        }
        }
        dp.add(depth, newSet);
    }
    return -1;
}

private int convert(int N, int repeat) {
    StringBuilder repeatedN = new StringBuilder();
    for (int i = 1; i <= repeat; i++)
        repeatedN.append(N);
    return Integer.parseInt(repeatedN.toString());
}

Related Posts